描述流体的运动是困难的。你如何开始谈论一个不规则的、复杂的粒子系统?大量的数学理论被创造出来试图确定流体的运动,从而产生了流体力学这个恰当命名的领域。流体力学属于更大的连续体力学领域,它有一些非常有趣、更广泛的概念。
流体力学的一个重要方面是涡量。涡度可以深入了解流体的旋转方式。在考虑刚体时,我们用不同的名称称涡量:角速度。然而,当我们处理的物质不是刚性的,比如流体时,它需要一种截然不同的处理方式。涡度本质上告诉我们流体内任何一点的局部旋转。
基础首先,让我们列出一些流体力学的基本定义。为简单起见,我将讨论限制在两个方面。定义流体的一种非常直接的方法是使用速度场。速度场将定义流体在流体内每个点的运动,并具有以下形式:


在这个速度场中,流体的运动只依赖于纵坐标。换句话说,所有具有相同y值的点都具有相同的速度。这提供了一种非常理想化但有用的数学描述流体的方法。现在,涡度呢?
涡度涡度是局部变量。这意味着它是为流体中的每个单独点定义的。看看上面的示例向量场,肯定有一些旋转在进行,但我们如何量化呢?这是涡量的定义
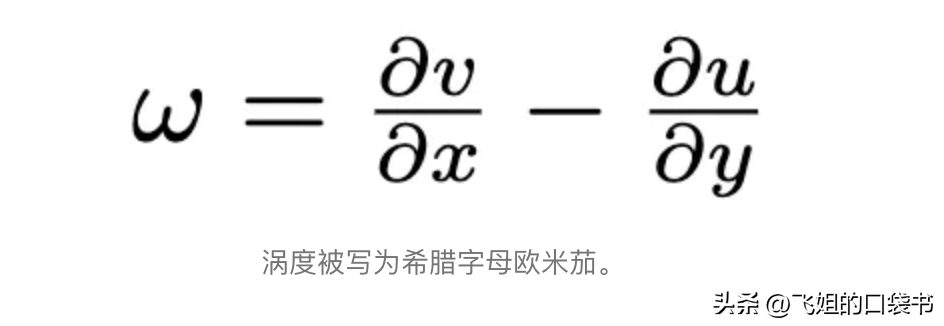
使用这个方程,我们可以定义上面矢量场的涡量。做这个计算,我得到ω=-5。这是什么意思?首先,我们可以考虑符号,负的涡度意味着顺时针旋转,我们可以在上面的矢量场中清楚地看到。数字5只是让我们了解旋转的强度。
关于获得ω=-5的涡度,一件非常有趣的事情是,这意味着流体中每个点的涡度都相同。这并非总是如此。同样,我们在这里大量简化了事情。大多数流体具有极其不同的矢量场和不同的涡度。

到目前为止,我们只是将流体中的涡度视为常数,但如果流体正在变化呢?当我们想知道天气将如何发展时,这在大气中尤为重要。我们可以从Navier-Stokes方程推导出称为涡量方程的东西。

如您所见,这很复杂!我不打算在这里定义所有术语,但希望这能让您了解流体力学的复杂性。
气氛要了解大气动力学,涡度是一个必不可少的工具。它变得更加复杂,因为地球本身也在旋转。大气科学家将区分坐标固定在地球表面的相对涡度和包括地球自转的绝对涡度。

这会变得更加复杂!涡量的符号和大小可用于预测某些天气事件。