几何最值问题综述:对于学生而言,刷了无数的题,总结了无数的解题方法,做了无数的笔记,积累了无数的错题,普遍认为初中平面几何问题中,最难是几何最值问题,而几何最值问题往往又与平面几何三大变化(平移变化、轴对称变化、旋转变化)相关。
几何最值理论依据有:①两点之间,线段最短。
②点到直线的距离,垂线段最短。
③三角形三边关系。
几何最值所用思想:转化思想
今天介绍隐形圆问题,隐形圆问题一共分5类:定点定长、四点共圆、定弦定角、定角定高、最大张角,本文介绍最基础的定点定长型。利用隐形圆求线段最值,最终都要用到:“一箭穿心”构图,一箭穿心是隐圆求最值问题的基础。
何为“一箭穿心”?先看一个图:
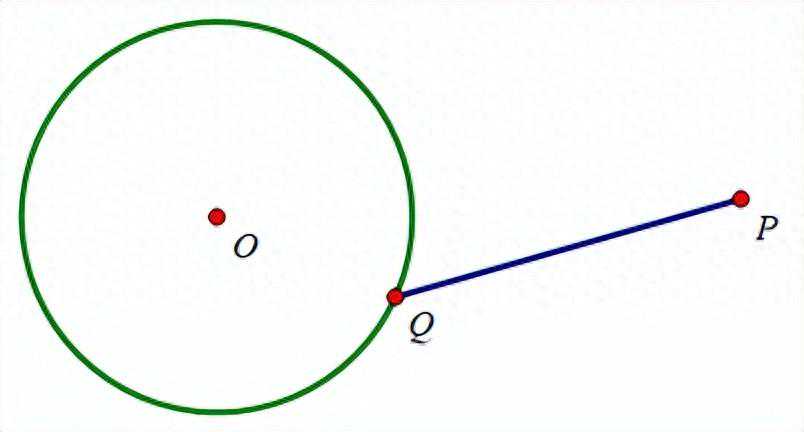
求PQ最大值,当点P,O,Q三点共线且点O在P,Q中间时,PQ长度最大,如图
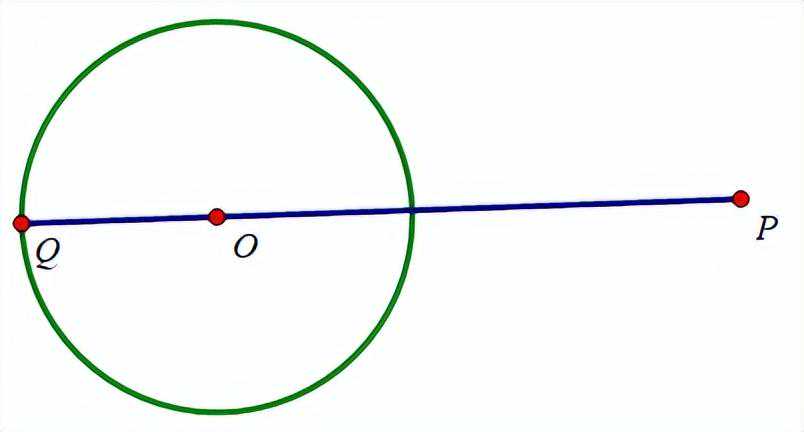
求PQ最小值,当点P,O,Q三点共线且点Q在P,O中间时,PQ长度最小,如图
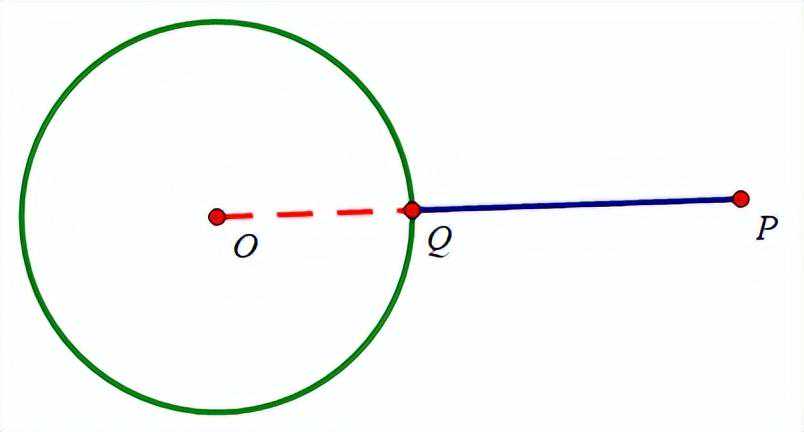
简而言之:求圆外一点到圆上的距离最值,圆外一点和圆上一点构成线段必过圆心,即一箭穿心。
定角定高型隐形圆问题:如图,直线BC外一点A,A到直线BC距离为定值(定高),∠BAC为定角,则AD有最小值,即△ABC的面积有最小值。因为其形像探照灯,所以也叫探照灯模型。
条件:在△ABC中,∠BAC=α(定角),AD是BC边上的高,且AD=h(定高)。
结论:当△ABC是等腰三角形(AB=AC)时,BC的长最小;△ABC的面积最小;△ABC的周长最小。
证明:如图,作△ABC的外接圆O,连接OA,OB,OC,
过点O作OE⊥BC于点H,设圆O的半径为r,则∠BOH=∠BAC=α
∴BC=2BH=2OB×sinα=2r×sinα
∵OA+OH≥AD(当且仅当点A,O,H三点共线时,等号成立)
∴r+rcosa≥h,
∴当取等号时r有最小值,此时BC的长最小:2r×sinα
∴△ABC的面积最小,△ABC的周长最小
典型题:
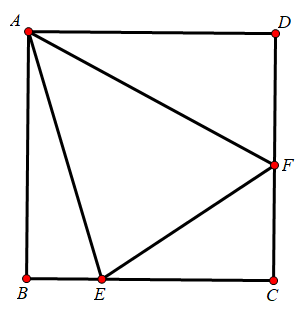
在四边形ABCD中,AB=AD=CD=4,AD∥BC,∠B=60°,点E、F分别为边BC、CD上的两个动点,且∠EAF=60°,则△AEF的面积的最小值是__________.
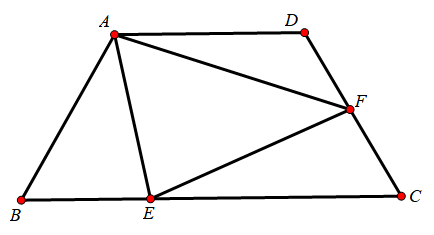
分析:该题破题关键是利用半角模型作出辅助线把△ADF逆时针旋转120°得到△ABF’,再过A作AM⊥CB于点M,AN⊥EF于点H,得到AH=AM(定高),∠EAF=60°(定角),因为是填空题,相关结论不再证明(前面已证),当AE=AF时,△AEF的面积最小。
解:辅助线如图所示(简写过程)
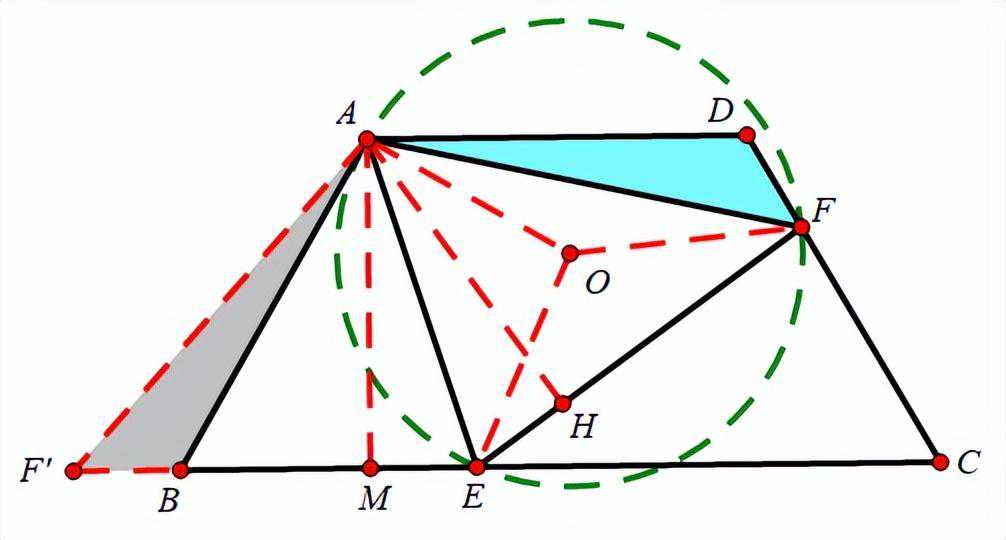
易得:点F’B,C三点共线,△AEF’≌△AEF
∴AH=AM(定高)
∴∠EAF=60°(定角)
∴符合定角定高型,当AE=AF时,△AEF的面积最小
∴此时△AEF为等边三角形
∴S△AEF最小=4√3
∴△AEF的面积的最小值是4√3
如图,正方形ABCD边长为8,E、F分别是边BC、CD上的动点,∠EAF=45°,则△AEF面积的最小值为________.