几何最值问题综述:对于学生而言,刷了无数的题,总结了无数的解题方法,做了无数的笔记,积累了无数的错题,普遍认为初中平面几何问题中,最难是几何最值问题,而几何最值问题往往又与平面几何三大变化(平移变化、轴对称变化、旋转变化)相关。
几何最值理论依据有:①两点之间,线段最短。
②点到直线的距离,垂线段最短。
③三角形三边关系。
几何最值所用思想:转化思想
今天介绍隐形圆问题,隐形圆问题一共分5类:定点定长、四点共圆、定弦定角、定角定高、最大张角,本文介绍最基础的定点定长型。利用隐形圆求线段最值,最终都要用到:“一箭穿心”构图,一箭穿心是隐圆求最值问题的基础。
何为“一箭穿心”?先看一个图:
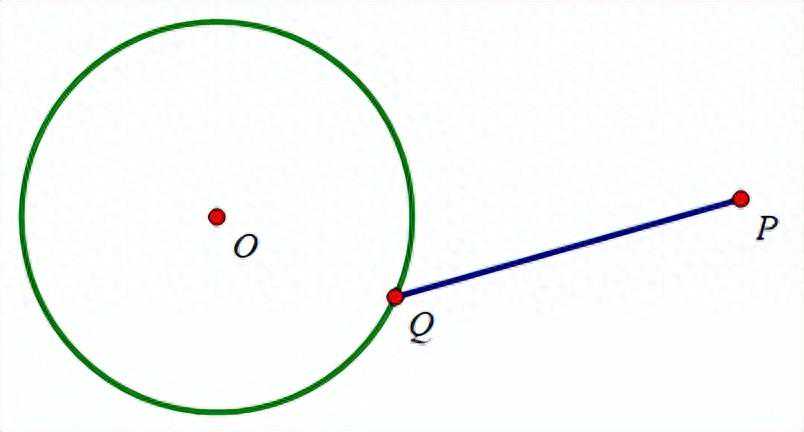
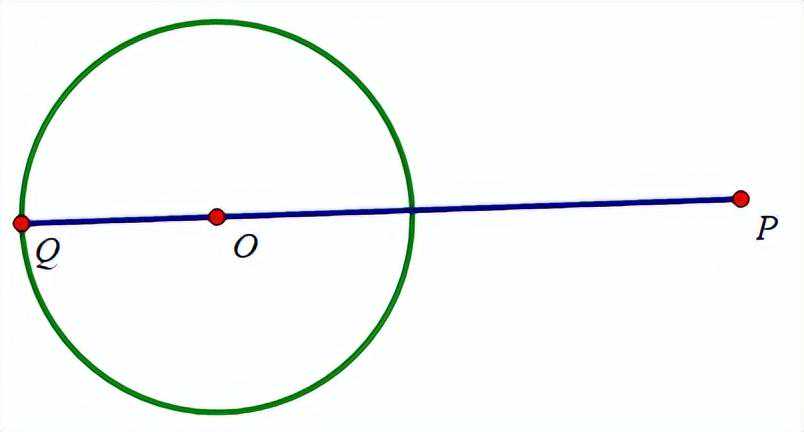
求PQ最大值,当点P,O,Q三点共线且点O在P,Q中间时,PQ长度最大,如图
求PQ最小值,当点P,O,Q三点共线且点Q在P,O中间时,PQ长度最小,如图
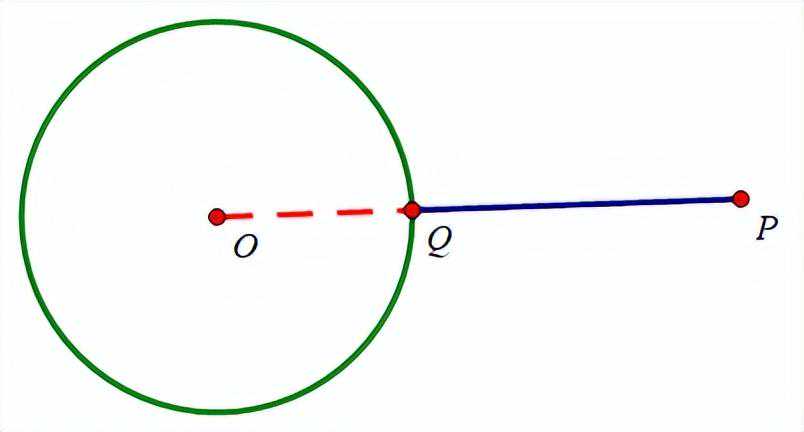
简而言之:求圆外一点到圆上的距离最值,圆外一点和圆上一点构成线段必过圆心,即一箭穿心。
定弦定角隐形圆问题:该问题和前面的四点共圆有重合的部分,区别是利用不在同一直线的三点确定一个圆。理论依据,圆的内接四边形对角互补、圆周角定理、三点定圆。只不过圆没有直接画出来,需要解题者自行画出圆来解决。
题型特点:
①存在对角互补的四边形。
②同弧(弦)等角。
③同弧所对两角成二倍关系
解题步骤:
1.画出隐形圆
2.利用一箭穿心构图,综合勾股定理,三角函数等知识解题。
典型题:
1、如图,四边形ABCD为矩形,AB=3,BC=4.点P是线段上一动点,
点M为线段上一点.∠ADM=∠BAP,求BM的最小值。
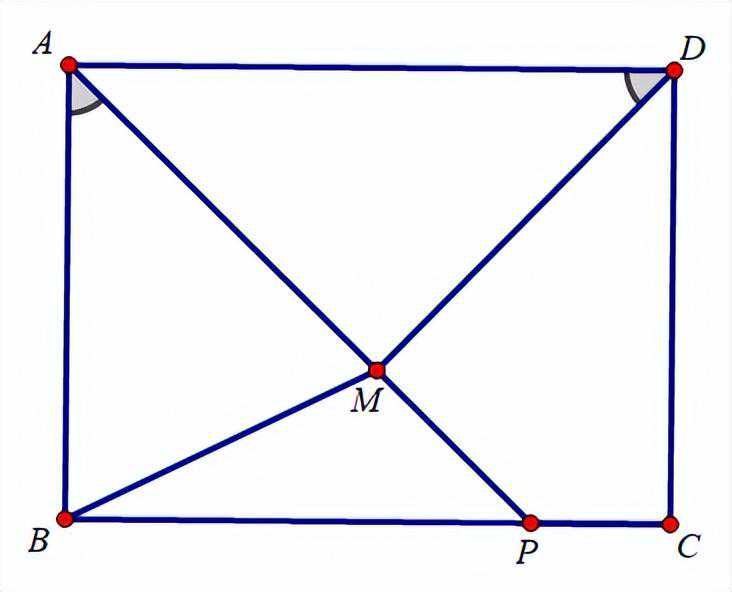
分析:∠ADM=∠BAP,四边形ABCD是矩形可得∠AMD是90°,AB=3,符合定弦定角。
解:辅助线如图所示,
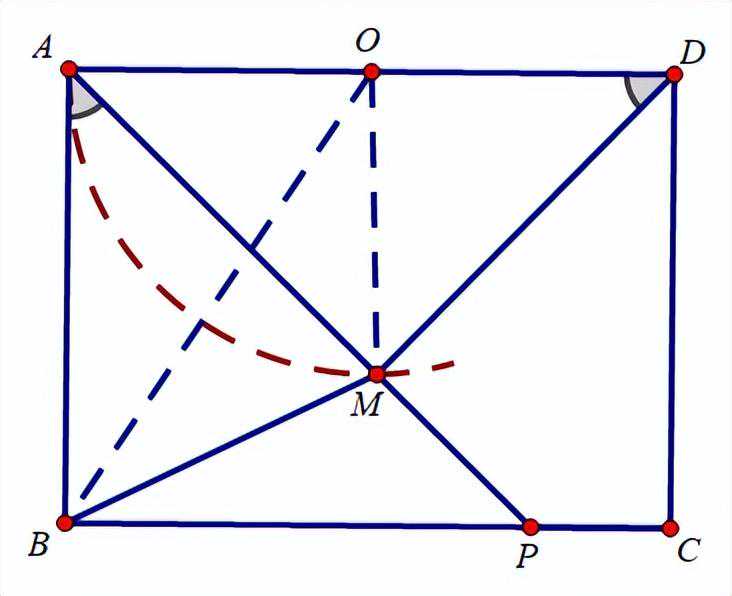
易得:点M在弧AM上运动,是圆O的一部分。
∵AB=3,BC=4
∴OA=2
∴OB=√13
当点B,M,O三点共线时,BM最小
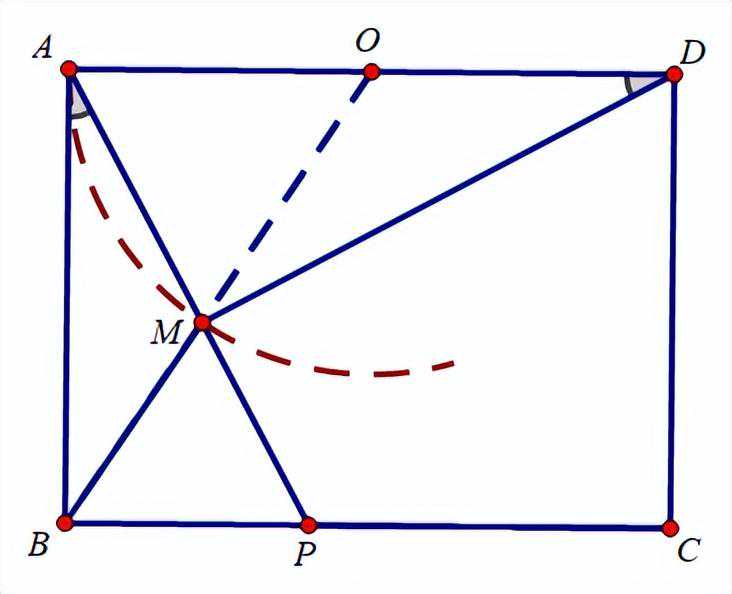
BM最小=√13-2
BM的最小值为√13-2
思考:求CM的最小值
2、已知等腰△ABC,∠ACB=120°,AC=BC=3,在平面内任作∠APB=60°,求BP最大值。
方法1:定弦定角解题
由已知条件易得AB是定值(定弦),∠ACB=120°,∠APB=60°(定角)是∠ACB=120°的一半,可以C为圆心,3为半径构造圆,如图
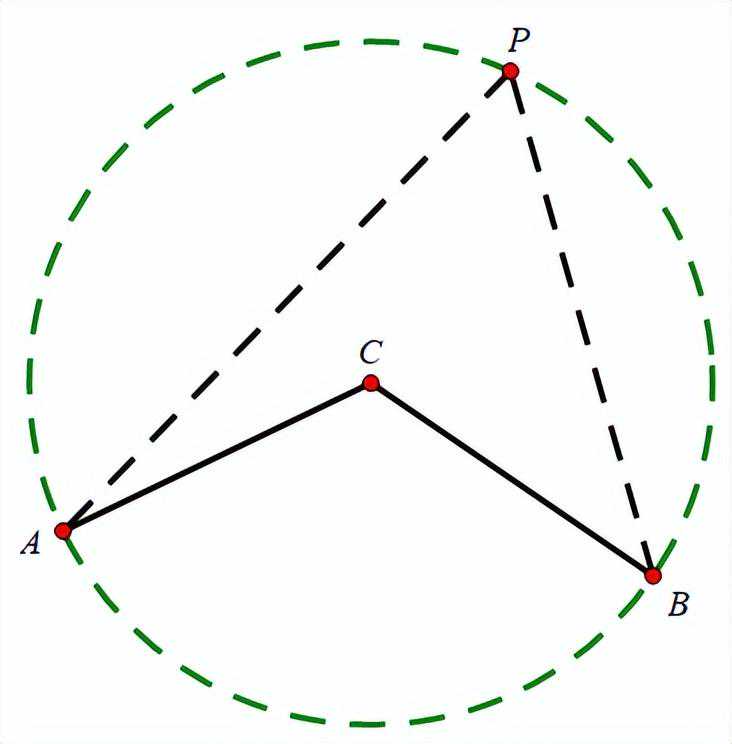
∴当BP是直径时取得最大值
∴BP的最大值是6
方法2:四点共圆解题
分析:∠ACB=120°,∠APB=60°可得:∠ACB和∠APB互补,则点A,B,P,C四点共圆
解:如图
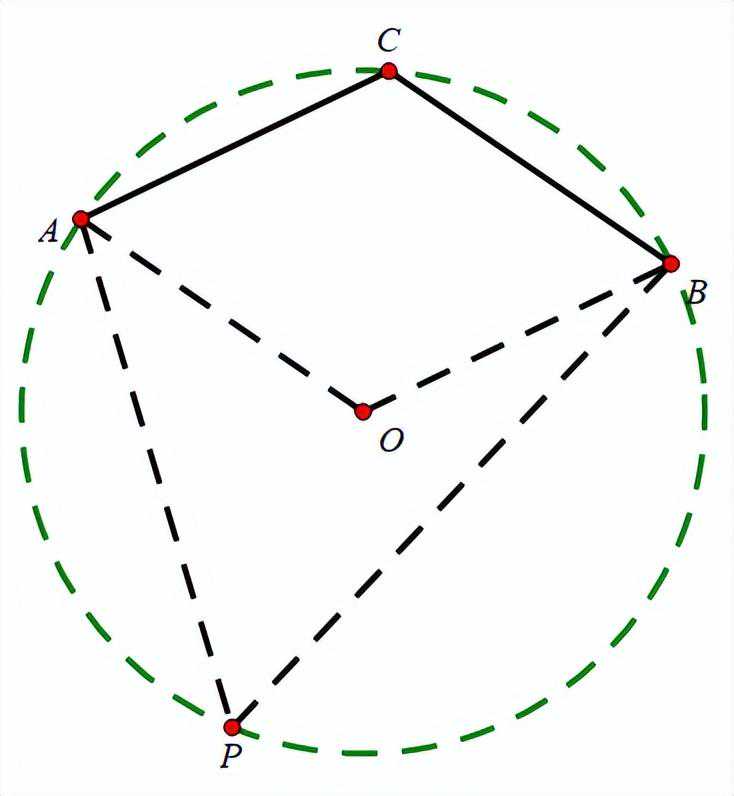
易得:圆O半径为3
∴当BP是直径时取得最大值
∴BP的最大值是6
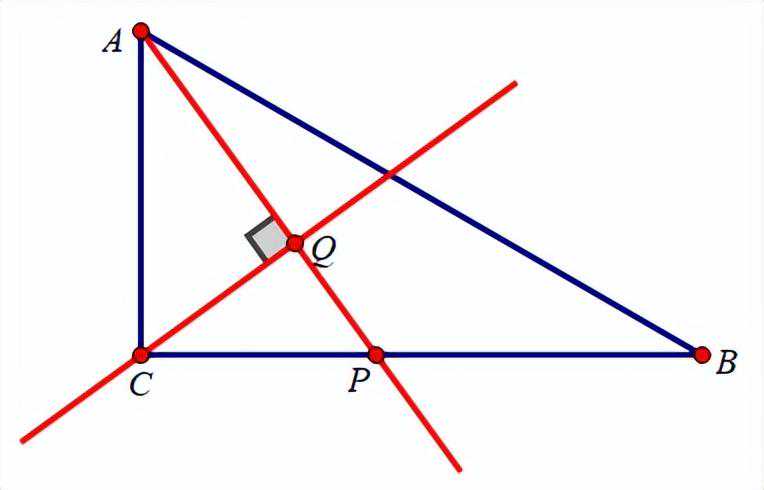
如图,Rt△ABC中,∠ACB=90°,∠CAB=60°,AB=4,点P是BC边上的动点,过点C作射线AP的垂线,垂足为Q,当点P从点C运动到点B时,点Q的运动路径长为_______