从以下方面介绍圆柱度:
1.数学定义(文末附带7.向量基础知识)
2.图纸标注
3.应用场合
4.取值方法
5.加工方法
6.测量方法
一、数学定义
马克思有句名言:一门科学只有在成功地运用数学时,才算达到了真正完善的地步。在ASME的GDT(GeometricDimensioningandTolerancing,几何尺寸与公差)标准体系中,就是在GDT中运用了数学。
圆柱度(Cylindricity)定义:圆柱度是指零件实际表面上所有的点,都在两个同轴的、几何学上理想的圆柱面所限定的空间内,这两个圆柱面的半径差由圆柱度公差确定。数学表达式为:
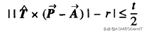
圆柱度的数学定义式
(1)
其中:
P带-是零件实际表面上的点;
T带^是圆柱轴的方向向量;
A带-是确定圆柱轴位置的位置向量,可看作是空间中的一个点,即圆柱轴上的一个点;
-是向量的减法运算符号;
x是向量的向量积符号;
||(里层的)符号表示求向量的模(大小),外层的是绝对值符号;
r是圆柱轴到公差带中分圆柱面的距离;
=是比较数值大小的“小于等于”符号;
t是圆柱度公差值,它决定了平行平面之间的距离;
t/2是t的二分之一。
式(1)的几何意义:到公差带中分圆柱面的距离小于等于t/2的所有点的集合。
判断零件的实际表面是否满足圆柱度公差要求,就在于判断是否存在T带^、A带-、r,使得该表面上的所有点P带-都满足式(1)。由于t是零件图纸(设计者)规定的,不能改变,为了找到T带^和A带-(它们共同确定空间中的轴线–圆柱轴),可以想象用半径很大的理想圆柱面,逐渐收缩到与实际轴上的6个高点形成接触(在此过程中,该理想圆柱面的朝向也会相应调整),此时,该理想圆柱面的轴线就确定了T带^和A带-。r的一种取值可以是该理想圆柱面的半径减去t/2(公差值的一半)。
关于6个高点接触的补充:不在一条直线上的3个点,可以确定一个圆。两组这样的点,就可以确定两个圆。这两个圆的圆心连线确定了圆柱面的轴线。
二、图纸标注
圆柱度在图纸上的标注方式及其含义见图3。
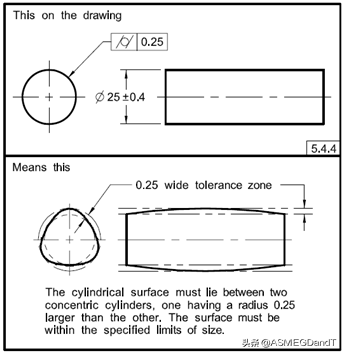
图1.圆柱度的标注及其含义
三、应用场合
圆柱度通常用在不旋转的场合:
1.圆柱形主基准特征
2.轴、孔配合
3.轴、孔定位
四、取值方法
本段假设不按的规则1#,即假设“包容原则”不是默认适用。
圆柱度如何取值?ISO标准体系中,对于机加工件,ISO2768-2(对应的国标GB/T1184)没有给出圆柱度的未注公差值。这是考虑到圆柱度同时包含了三项:圆度、直线度和平行度。这三项在ISO2768-2中都有未注公差规定。
由于几何学上的原因,这三项的综合公差值(圆柱度值)会小于三项公差之和。但在实际工作中,可以简单化处理,即在从功能角度考虑问题,以便决定是否注出包容要求或圆柱度要求时,直接考察三项公差之和。
如果功能上要求某特征的圆柱度必须小于上述综合公差值,则需要单独注出圆柱度。如果只是配合功能,则可能应用“包容原则”就行了。
圆度、直线度、平行度的未注公差简要说明如下:
圆度:直径公差,且不大于跳动公差。直线度:与平面度共用一张表。平行度:等于尺寸公差和平面度/直线度公差中的大者。
圆柱度注出值参考表1和图2.
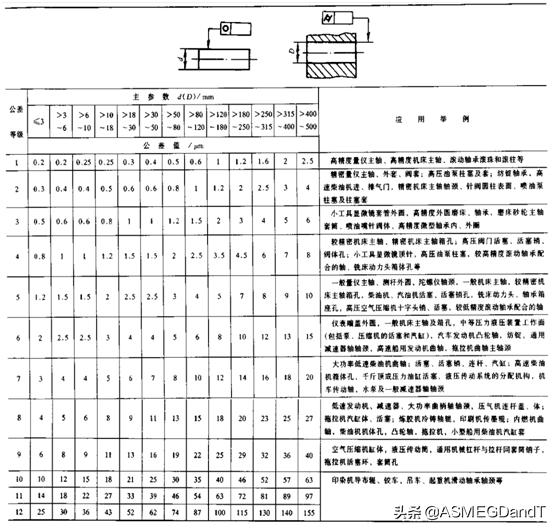
表1.圆柱度公差值及应用举例
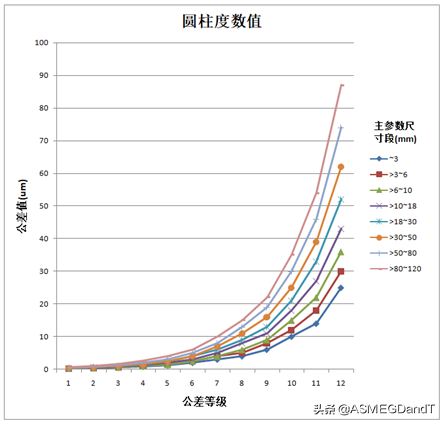
图2.圆柱度数值
根据实测及分析,在一般加工条件下,圆柱度误差占尺寸公差的30%以下,只有少数情况大于50%。也就是说,一般加工方法在保证尺寸公差的同时,也必然能保证相应的圆柱度精度。从图纸传达设计意图的角度看,这并不意味着可以由尺寸公差代替圆柱度。只是工艺上可能不必采取特别措施。
五、加工方法
外圆表面(轴)的常用加工方案:车削类、车磨类、特种加工类。
内圆表面(孔)的常用加工方案:车(镗)类、车(镗)磨类、钻扩铰类、拉削类和特种加工类。
常用加工方法能达到的圆柱度公差等级如表2.
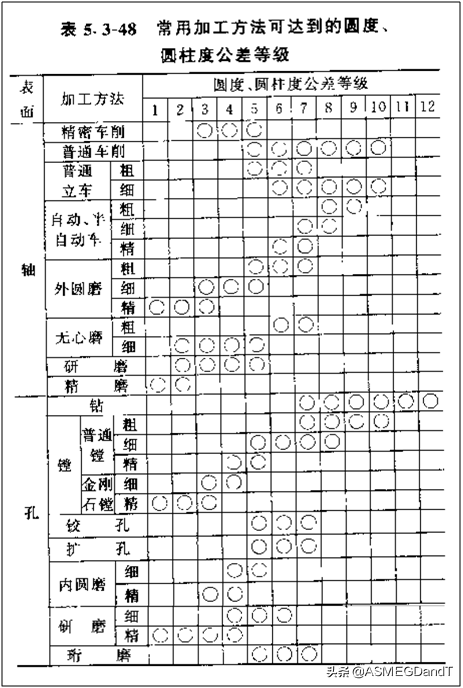
表2.加工方法可达到的圆柱度公差等级
零件的切削加工往往不是一次到位的,而是逐步减少背吃刀量分阶段完成的。切削加工可分为5个阶段:粗加工、半精加工、精加工、精密加工、超精密加工。不过请注意,对于绝大多数零件,一般只经过前三个阶段,到精加工为止。
切削加工划分阶段能带来的优点有:
(1)避免毛坯内应力的释放影响加工精度。毛坯粗加工一遍,待内应力释放平衡后再精加工,即可减少内应力释放导致的精度丧失。
(2)粗加工时,背吃刀量较大,因此切削力大,需要的夹紧力也大,这些都会引起弹性变形和热变形,从而影响零件精度。粗加工提高生产效率,精加工保证精度。
(3)粗加工时发现、暴露的毛坯缺陷,有助于尽早决定取舍,避免浪费。
(4)粗加工可安排在精度较低的机床上(成本也较低)。精密机床仅用于精加工,也有利于机床长期保持较高精度。
(5)便于有些零件需要安排热处理工序。
六、测量方法
圆柱度的测量方法见图3:
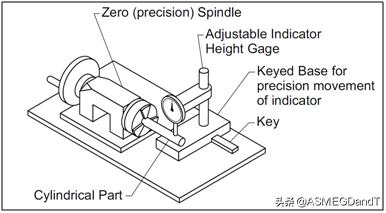
图3.圆柱度测量方法
首先测量轴的尺寸,合格之后,再挑几个位置,沿轴向全长测量一下,最后一边旋转轴,一边沿轴向移动千分表。
七、向量基础知识
1.物理学知识告诉我们,力有大小和方向。类似这样既有大小,又有方向的量,叫做向量。
2.在数学上,大小可以用线段的长度表示,方向用线段的朝向来表示。这样,有向线段就可以表示向量。
3.与起点无关的向量,称为自由向量。两个向量只要大小相等,且方向相同,则经过平移之后,总能完全重合,因此它们是相等的。
4.向量的大小叫做向量的模。模等于1的向量叫做单位向量。
5.模相同而方向相反(成180度)的向量互为正、负向量。
6.两个向量的加法(和)运算,参照力学上求合力的平行四边形法则。
7.两个向量的减法(差)运算,其实就是加上负向量。
8.在空间直角坐标系Oxyz中,根据勾股定理,容易知道向量(x,y,z)的模r=(x^2+y^2+z^2)^0.5。
9.方向向量是一个单位向量。直线的方向向量是与直线平行的向量。
10.两个向量的向量积,参照物理学上的力矩(力乘以力臂,力臂是力的作用线到转动轴的垂直距离),即三者的乘积:力的大小、位移的大小、力与位移夹角的正弦。向量积的方向垂直于该两个向量所决定的平面,其指向按右手规则:右手的四个手指从第一个向量朝第二个向量握拳时(不超过180度),大拇指的指向。



